Absolute Value Calculator

The calculator solves the equation by displaying the graph, the solution’s integer values, and their number line representation. Here you can see the graph of equation \( y = |x| \):

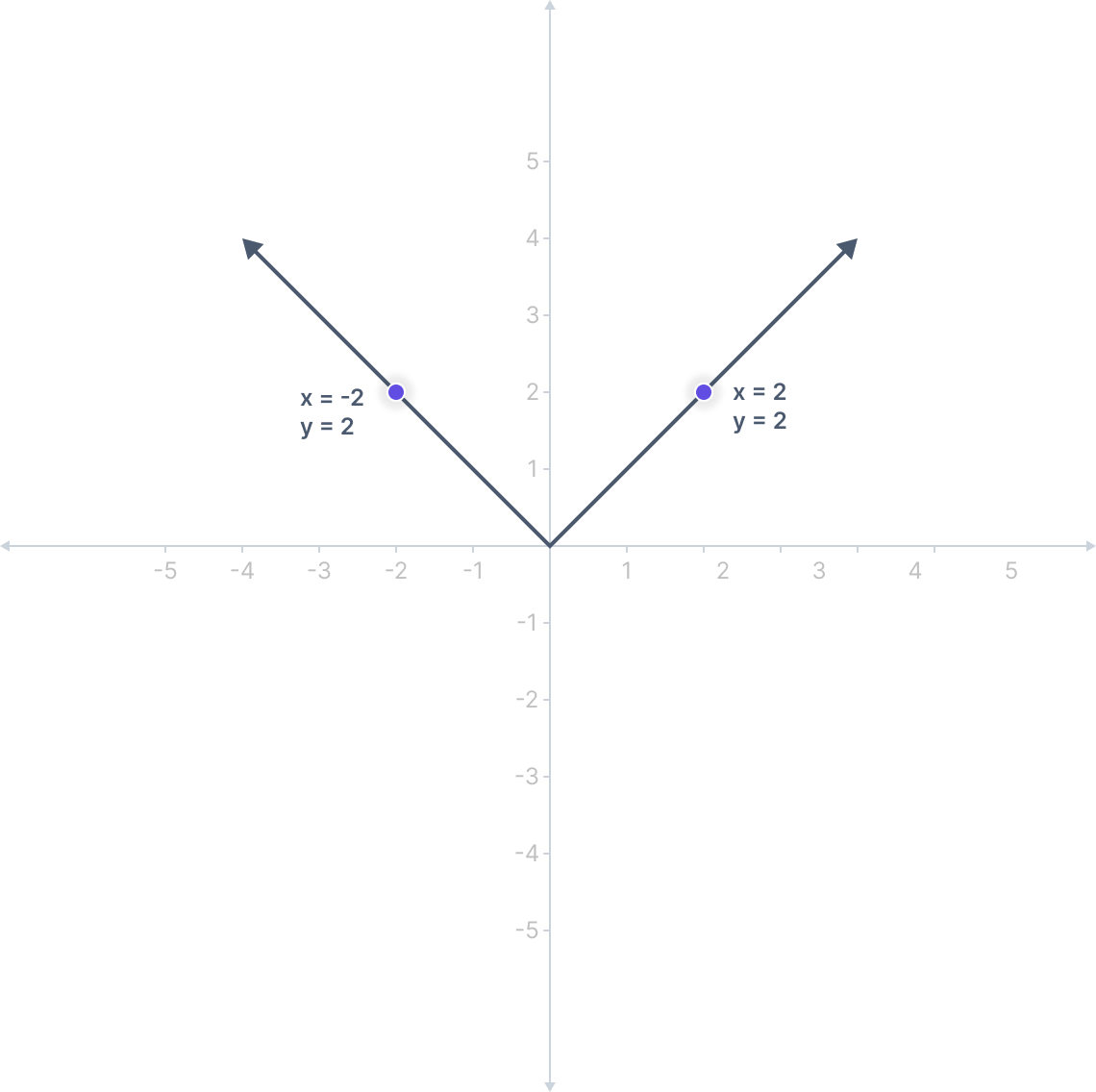
Here you can see, whether x = 2 or x = -2, but absolute value of x is 2 in both cases.

What are Absolute Value Equations?

Absolute value equations are those that contain variables inside the absolute operator (modulus). In mathematics, an equation with an absolute value expression is known as an absolute value equation.

For instance,\( |x+1|=2\). Here, the absolute expression is \(|x+1|\). The absolute value shows how far away from zero the given integer is. Negative numbers are not permitted in this case. It is the magnitude or size of the number.

For eg., \(|-2| = 2\)

Since \(-2\) is 2 less than the value 0, it. As a result, \(-2\) has an absolute value of 2. These equations are applied to various real-world issues, including estimating distance, figuring out range, variance, etc.

How to graph absolute value function?

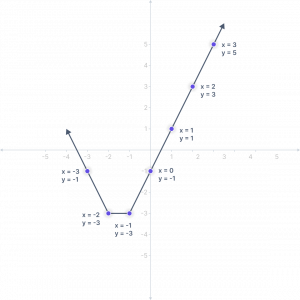
Example 1: Consider the equation: \( y = |2x + 3| – 4 \)

To graph this equation, first, we need to find y by assuming values for x. Here we will consider x = -3, -2, -1, 0, 1, 2, 3.

For x = -3, \( y = |2(-3) + 3| – 4 = |-6 + 3| – 4 = |-3| – 4 = 3 – 4 = -1 \)

For x = -2, \( y = |2(-2) + 3| – 4 = |-4 + 3| – 4 = |-1| – 4 = 1 – 4 = -3 \)

For x = -1, \( y = |2(-1) + 3| – 4 = |-2 + 3| – 4 = |-1| – 4 = 1 – 4 = -3 \)

For x = 0, \( y = |2(0) + 3| – 4 = |0 + 3| – 4 = |3| – 4 = 3 – 4 = -1 \)

For x = 1, \( y = |2(1) + 3| – 4 = |2 + 3| – 4 = |5| – 4 = 5 – 4 = 1 \)

For x = 2, \( y = |2(2) + 3| – 4 = |4 + 3| – 4 = |7| – 4 = 7 – 4 = 3 \)

For x = 3, \( y = |2(3) + 3| – 4 = |6 + 3| – 4 = |9| – 4 = 9 – 4 = 5 \)

Now we found these sets of (x, y): (-3, -1), (-2, -3), (-1, -3), (0, -1), (1, 1), (2, 3) and (3, 5). We can use these values to draw a graph. So, the graph for \( y = |2x + 3| – 4 \) will be:

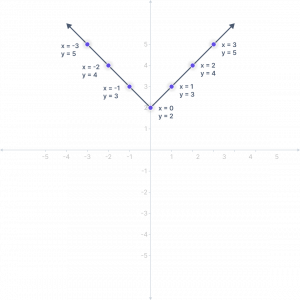
Example 2: Consider the equation: \( y = |x| + 2 \)

For x = -3, \( y = |-3| + 2 = 3 + 2 = 5 \)

For x = -2, \( y = |-2| + 2 = 2 + 2 = 4 \)

For x = -1, \( y = |-1| + 2 = 1 + 2 = 3 \)

For x = 0, \( y = |0| + 2 = 0 + 2 = 2 \)

For x = 1, \( y = |1| + 2 = 1 + 2 = 3 \)

For x = 2, \( y = |2| + 2 = 2 + 2 = 4 \)

For x = 3, \( y = |3| + 2 = 3 + 2 = 5 \)

Now we found these sets of (x, y): (-3, 5), (-2, 4), (-1, 3), (0, 2), (1, 3), (2, 4) and (3, 5). We can use these values to draw a graph. So, the graph for \( y = |x| + 2 \) will be:

How to Use the Absolute Value Calculator?

Follow these steps to use the Absolute Value Calculator:

• Type the equation into the text box.
• To obtain the outcome, press the “Solve” button now.
• The equations for absolute values will then be shown.

The calculator is dependable and effective because it gives you the most precise and correct answers. Moreover, this calculator is free, in contrast to other online tools. It functions in your browser and doesn’t need to be downloaded or installed. Its user interface is simple, making it easy for anyone to use and navigate.

FAQs