Dot Product Calculator

Our Dot Product Calculator prioritizes simplicity and dependability over speed. This program guarantees the accuracy of each computation, giving you quick, reliable outcomes. Our calculator is made to effectively work for you whether you’re doing homework, getting ready for an examination, or handling job-related duties.

Anyone can utilize the Dot Product Calculator due to its outstanding user-friendliness. Anyone may easily use this tool, regardless of expertise level. Feel the shift in your approach to solving mathematical issues, which will improve the efficiency and productivity of your workflow. Upgrade your mathematical abilities by adopting this advanced Vector Dot Product Calculator right away!

What is the Definition of Dot Product?

The Dot Product is the name given to the scalar value in mathematics that derives from specific calculations carried out on the vector components. The dot product of two vectors is represented by the thick dot.

Method to Determine Dot Product

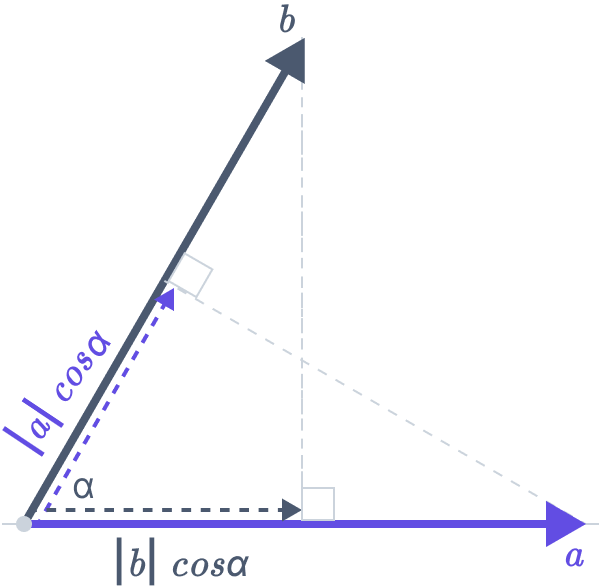
If two vectors are a and b, the method used to determine their dot product is as follows:

\( a·b = |a|·|b|·cos(θ) \)

Where:

• |a| and |b| are the magnitude of the vectors
• θ is the angle between the vectors

When cosine is the proportion of the scalar product to the magnitudes of the vectors, the calculator can also be used to determine the angle between two vectors:

\( cos(θ) = \dfrac{a × b}{|a| × |b|} \)

Read More about the Dot Product of Two Vectors.

Characteristics of the Dot Product

The dot product, or scalar product, is a fundamental operation involving vectors. Here are its key characteristics:

Commutative Characteristic

The dot product obeys the commutative law, which states that for any vectors →a and →b, the result of their dot product remains constant regardless of their order:
→a · →b = →b · →a
This indicates that the outcome of the dot product does not depend on the sequence of the vectors.

Distributive Characteristic

The dot product also adheres to the distributive law over the addition and subtraction of vectors:
→a · (→b + →c) = →a · →b + →a · →c
→a · (→b – →c) = →a · →b – →a · →c
This characteristic means that the dot product can be distributed across the addition or subtraction of vectors.

Dot Product Nature

The nature of the dot product is closely related to the angle θ between the two vectors →a and →b:
If θ = 0, then →a · →b = |→a| |→b| cos θ = |→a| |→b|.
If θ = π, then →a · →b = |→a| |→b| cos θ = – |→a| |→b|.
If θ = π/2, then →a · →b = |→a| |→b| cos θ = 0.
If 0 < θ < π/2, then →a · →b > 0 (both vectors point in the same general direction).
If π/2 < θ < π, then →a · →b < 0 (both vectors point in opposite directions).

Dot Product To sum up, the dot product’s sign and magnitude reveal details about the corresponding positions of the vectors:

• Vectors that point in the identical direction are shown by a positive dot product.
• When the dot product is negative, it signifies that the vectors are pointing in opposite directions.
• The vectors are perpendicular if the dot product is zero.

Vector Dot Product Calculator

The cross product, indicated by the sign “×,” and the dot product, also referred to as the scalar product and indicated by the symbol “,” are the two fundamental kinds of scalar multiplication. According to the Vector Dot Product Calculator, the dot product yields a single number as its product, but the cross product yields a vector.

Method for Finding the Dot Product of Two Vectors (Dot Product of Two Vectors Calculator)

A dot product is the total of the products in the cartesian location of two vectors. Unlike the cross product (which is a vector), the dot product also referred to as ab, is just one number.

The two vectors are perpendicular or orthogonal to each other if their dot product equals 0.

Solved Example of Vector Dot Product Calculator

Example 1: Find the dot product of the vectors A and B.
A = 3i + 2j – 5k
B = -6i + 4j + 2k

We need to use the component formula for the dot product of three-dimensional vectors here,

\( a⋅b = a_1 b_1 + a_2 b_2 + a_3 b_3 \)

The dot product is:

\( a⋅b = 2(5) + 3(−6) + 4(7) = 10 − 18 + 28 = 20\)

Dot product = 20

Example 2: Calculate the dot product of: a = (2, 3, 4) and b = (5, −6, 7)

The dot product of two vectors A and B is given by the sum of the products of their corresponding components:
A · B = (3i + 2j – 5k) · (-6i + 4j + 2k)

Now, calculate the dot product:
A · B = 3(-6) + 2(4) + (-5)(2)
A · B = -18 + 8 – 10
A · B = -20

So, the dot product of vectors A and B is -20.

Frequently Asked Questions for Dot Product Calculator