Discriminant Calculator

Discriminant Formula for Quadratic Equation

The discriminant formula for the quadratic equation \(ax^2 + bx + c = 0\), where \( a ≠ 0 \), is \(b^2 – 4ac \).

The discriminant is also represented by the symbol \(Δ\).

\(∴ Δ = b^2 – 4ac \)

Make your calculations simple and easy using an online discriminant calculator from mathematics master to get your results with the snap of the hand.

Graphs of \( y = ax^2 + bx + c \)	Discriminant	Number of types and solutions
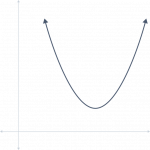	Discriminant is negative	No x-intercepts No Roots Two imaginary solutions
	Discriminant is zero	One x-intercept One Root (a double root) One real solution
	Discriminant is positive	Two x-intercepts Two Roots Two real solutions

Define Discriminant

It is the root that leads to quadratic equations and defines the characteristics, types, and differences. The equation can differentiate between the following types of answers.

• In the value with positive discriminant, we get two real solutions.
• For zero discriminant value there i one real solution.
• In the negative value, there are two complex solutions.

What does discriminant in Maths stand for?

The value used to assess the types of solutions in incorporating the quadratic formula is known as the discriminant. It is the unique feature of quadratic equations coefficient that provides information regarding roots.

The discriminant differentiates between three types different types of quadratic equation solutions.

Case 1: If the discriminant D exceeds 0, we can take the square root and get two valid answers.

Consider a=2, b=5, c=3

\( =b^2-4ac \)

\(=(5)^2-4(2)(3) \)

\(=25-24 \)

\(= 1\)

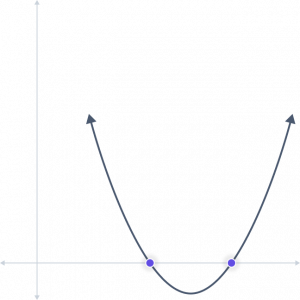
Case 2: There is only one real solution if the discriminant D equals 0, which may be found by taking the square root of 0.

Consider a=4, b=4, c=1

\( =b^2-4ac \)

\(=(4)^2-4(4)(1) \)

\(=16-16 \)

\(= 0\)

Case 3: If the discriminant D is smaller than 0, we can get two complex solutions by taking the square root of a negative number.

Consider a=1, b=4, c=6

\( =b^2-4ac \)

\(=(4)^2-4(1)(6) \)

\(=16-24 \)

\(= -8\)

How to calculate discriminant with the aid of a discriminant calculator?

Follow the instructions below to use the discriminant calculators.

1. Select the polynomial degree ranging from 2-5 that includes quadratic, quartic, cubic, and quintic polynomials. (degrees 2, 3, 4, 5).
2. To calculate the discriminant of quadratic equations choose second degree and proceed.
3. Put all your polynomial coefficients including the coefficient with zero values in the equation.
4. To get the outcome click solve.
5. The discriminant value will be available in the output field.

FAQs