Significant Figure Rules

For instance, the number \(12.3\) is said to possess \(3\) significant figures since three digits are known to be reliable. But on the other hand, when analyzing the number \(11.20\), it is said to contain four significant figures, as all four digits contribute to the precision of the value.

Let’s envision a scenario where you approach a fruit vendor and request \(437.8216\) grams of apples. Regardless of your intentions, it is highly likely that the vendor would react with bewilderment. In our daily routines, such a meticulous level of accuracy is neither necessary nor practically attainable. This is where significant figure rules come to our aid, enabling us to simplify and convey numbers more conveniently. 

By utilizing significant figures, we can ensure practicality and simplify our interactions in various real-life situations, such as purchasing fruits from a vendor. You can use Sig Fig Calculator, provided by The Mathematics Master.

What are significant figures?

• Significant figures are essential for representing numbers meaningfully and establishing their numerical value. To determine the number of significant figures, one should count all the digits starting from the first non-zero digit on the left.
• These significant figures are crucial for accurately expressing quantities, such as length, volume, mass, and measurements. They enable us to convey the precision and reliability of these quantities effectively.
• In mathematical calculations involving significant figures, operations such as addition, subtraction, multiplication, and division are employed to maintain the appropriate level of accuracy and preserve the significant figures throughout the computation.

Significant Figures Rules

It is crucial to adhere to certain rules to determine the significant figures in a calculated measurement. Now, let’s delve into the specific rules that govern the determination of significant figures:

• Non-zero digits are significant.
• For instance, in the measurement \(8565\) cm, there are four significant figures, and in \(0.345\), there are three significant figures.
• Preceding zeroes before a non-zero digit are not significant.
• These preceding zeroes merely indicate the position of the decimal point. For example, in the number \(0.003\), there is only one significant figure, and the number \(0.00134\) has three significant figures.
• Zeroes between two non-zero digits are significant.
• For example, in the value \(2.4008\), there are five significant figures.
• Zeroes at the end or on the right side of a number are significant.
• In the case of \(0.400\), there are three significant figures.

By following these rules, one can accurately determine the significant figures in a calculated measurement and convey the precision of the measured quantity.

Significant Figures Rules for Multiplication & Division

• When performing multiplication, a fundamental principle governs the usage of significant figures: the precision of the final result is limited by the least precise measurement involved.
• It is important to consider the significant figures in each measurement rather than the number of decimal places. When multiplying multiple observations, the result can only retain significant figures up to the least precise measurement, ensuring accuracy in the outcome.

The same rule applied to Significant figure rules for division.

Example

Let’s consider the example of multiplying \(2.3\) by \(1.56\).

Step 1: Determine the number of significant figures in each factor.

• The number \(2.3\) has two significant figures.
• The number \(1.56\) has three significant figures.

Step 2: \(2.3\) x \(1.56 = 3.588\).

Step 3: Since the least precise measurement involves two significant figures \((2.3)\), we must round the result accordingly.

Step 4: Round the result to match the least number of significant figures. In this case, the result \(3.588\) must be rounded to two significant figures.

Step 5: The digit following the second significant figure is \(8\). Therefore, we round up the second significant figure \((8)\) to \(9\).

Step 6: After rounding, the final result is \(3.6\), with two significant figures.

Significant Figure for Multiplication

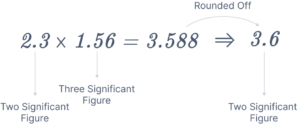
Significant Figure Rules for Addition & Subtraction

To round off the result in addition and subtraction, we consider the last common digit that appears furthest to the right in all components involved. Alternatively, we can express this rule as follows: the result is rounded off to match the number of digits of the measurement with the fewest decimal places, counting from left to right.

Examples

Let’s consider the example of adding \(12.345\) and \(0.0028\).

Step 1: Determine the number of decimal places in each number.

• The number \(12.345\) has three decimal places.
• The number \(0.0028\) has four decimal places.

Step 2: In this case, we need to align the decimal places by moving the decimal point in \(12.345\) four places to the right, resulting in \(12.3450\).

Step 3: \(12.3450 + 0.0028 = 12.3478\).

Step 4: Since the least precise measurement involves three decimal places \((0.0028)\), we must round the result accordingly.

Step 5: In this case, the result 12.3478 must be rounded to three decimal places.

Step 6: Apply rounding rules.

• The digit following the third decimal place is \(7\), greater than or equal to \(5\). Therefore, we round up the third decimal place \((7)\) to \(8\).

Step 7: After rounding, the final result is \(12.348\), with three decimal places.

Significant Figure For Addition

Conclusion

• Significant figures are necessary to represent numerical values in digit form accurately.
• In a given question or calculation, the number of significant figures in the result is determined by the quantity with the fewest significant figures. The least number of significant figures among all the quantities involved dictates the precision of the final answer.