Slope Calculator

The absolute value of a line’s slope, m, is typically used to determine how steep it is. The line becomes steeper as the value increases. Based on the sign and value of m, one can deduce the direction of the line that m describes:

The slope calculator helps determine the slope of any line between two locations.

Slope formula

The slope formula is ‘rise over run’. It can be written as:

\( m = \dfrac{(y_2 – y_1)}{(x_2 – x_1)} \)

\( m = \dfrac{𝚫y}{𝚫x} \)

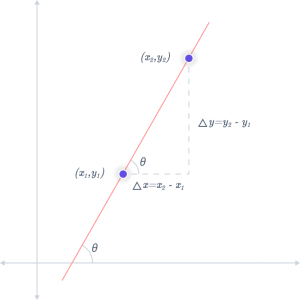
Find the Slope of a Line

For example, let’s find the slope of a line that passes through points (4, 3) and (12, 8).

Start with the slope formula: \( m = \dfrac{(y_2 – y_1)}{(x_2 – x_1)} \)

Replace the x and y values with the coordinate‘s x and y values.

\( m = \dfrac{(8 – 3)}{(12 – 4)} \)

Solve to find the delta of x and y.

\( m = \dfrac{(8 – 3)}{(12 – 4)} \)

\( m = \dfrac{5}{8} \)

So, the slope m is equal to \(\dfrac{5}{8} \)

How to Find Equations of a Line Using the Slope

For example, let’s solve for b, given a slope of \( \frac{1}{2} \) and a point (6, 5).

Slope Intercept Form: \( y = mx + b \)

Substitute for m:

\( y = (\dfrac{1}{2} × x) + b \)

Substitute the values for x and y:

\( 5 = (\dfrac{1}{2} × 6) + b \)

Solve for b:

\(  5 = 3 + b \)

\(  5 – 3 = b \)

\(  2 = b \)

Substitute the value of b in the equation to find the slope intercept form:

\( y = (\dfrac{1}{2}x) + 2 \)

How to Find Point-Slope Form

For example, let’s express the same line from the previous example using the point-slope form. Recall that the line has a slope of 1/2 and a point (8,6). (5,4)

Point-Slope Form: \( y – y_1 = m(x – x_1) \)

Substitute for m:

\( y – y_1 = \dfrac{1}{2}(x – x_1) \)

Substitute the values for x and y:

\( y – 6 = \dfrac{1}{2}(x – 8) \)

So, the point-slope form for this line is \( y – 6 = \dfrac{1}{2}(x – 8) \).

How to Find Standard Form

For example, let’s find the x and y intercepts of the line \( y = \dfrac{1}{2}x + 5 \)

Standard Form: \( Ax + By = C \)

Start by setting x to 0.

\( y = (\dfrac{1}{2} × 0) + 5 \)

Then solve for y

\( y = 5 \)

When x is equal to zero, y is equal to 5, so 5 is the y-intercept.

Next, set y to 0.

\( 0 = \dfrac{1}{2}x + 5 \)

Then solve for x

\( 0 = \dfrac{1}{2}x + 5 \)

\( 0 – 5 = \dfrac{1}{2}x + 5 -5 \)

\( -5 = \dfrac{1}{2}x \)

\( \dfrac{-5}{1} = \dfrac{1}{2}x \)

\( \dfrac{-5 × 2}{1} = \dfrac{1 × 2}{2}x \)

\( \dfrac{-10}{1} = \dfrac{2}{2}x \) -10/1 = 2/2x

\( -10 = x \)

When y is equal to zero, x is equal to -10, so the x-intercept is -10.

FAQs