Slope Intercept Form

The slope-intercept form provides a formula to graph a line on a coordinate plane using the X and Y axes. This form of the equation incorporates two essential pieces of information:

Slope: The slope on the graph determines the line’s angle, direction, and steepness.

Intercept: The intercept represents the point at which the line intersects the y-axis.

The significance of these two properties contributes to the name of this linear equation form, the slope-intercept form. It is widely used and recognized as the most common representation of straight lines.

Read more about Slope Calculator.

Slope Intercept Formula

The slope intercept formula takes the following general structure:

\(y = mx + b\)

In this form:

• \(“m”\) represents the slope of the line, indicating its steepness or inclination.
• \(“b”\) represents the y-intercept, where the line intersects the y-axis.

The variables \(“x”\) and \(“y”\) represent any point on the line, allowing flexibility in calculating values.

When utilizing this formula, retaining \(“x”\) and \(“y”\) as the variables are important to apply the slope-intercept form effectively.

Here are some linear equations presented in slope-intercept form as examples:

• \(y = 2x + 3\)
• \(y = -0.5x + 2\)
• \(y = 0.2x – 1.5\)

Conversely, the following linear equations are not in slope-intercept form:

• \(3x + 2y = 5\)
• \(4x – 2y = 8\)
• \(5y – 10x + 15 = 0\)

The equations explicitly represent the slope and y-intercept in slope-intercept form, facilitating a clear understanding of the line’s properties. However, the equations not in slope-intercept form require further manipulation to determine the slope and intercept.

Point-Slope Form and Slope-Intercept Formula of a Linear Equation

When determining the equation of a line, two variations of the general form can be employed. These formulas are as follows:

• Point Slope Formula: \((y – y_1) = m(x – x_1)\)
• Slope-Intercept Formula: \(y = mx + b\)

The choice between these forms is contingent upon the information provided at the outset, as the names of the formulas suggest. 

For example, the Point Slope Formula is suitable if you are given a point on the line \((x_1, y_1)\) and its slope \((m)\). 

On the other hand, if you have the slope \((m)\) and the y-intercept \((b)\), the Slope-Intercept Formula is the appropriate choice.

Derivation of Slope Intercept Form of an Equation

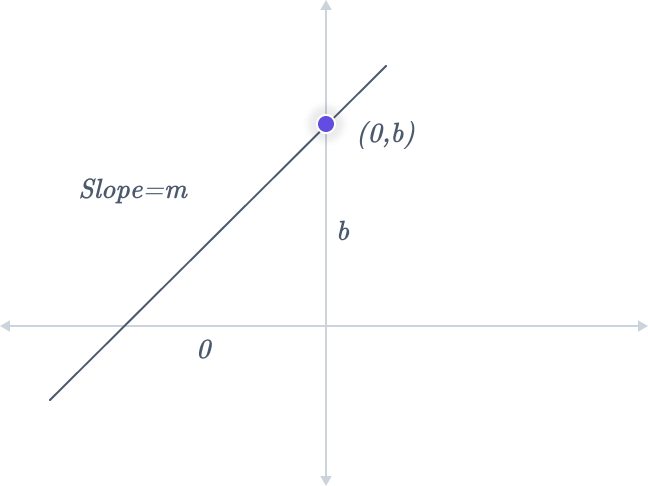
Let’s explore the process of deriving the slope-intercept form equation of a straight line through the following steps:

Step 1:

Consider a line, A, with a slope, m, and a y-intercept, b. Identify the point that must lie on the line.

The point that includes the y-intercept is \((0, b)\).

Step 2:

Recall that formula for slope is the ratio of the change in y to the change in x. 

Complete the equation for the slope, m, using the y-intercept \((0, b)\) and another point \((x, y)\) on the line.

Slope, \(m = \dfrac{change\space in\space y-values}{change\space in\space x-values}\)

Slope, \(m =\dfrac{y – b}{x – 0}\)

Slope, \(m = \dfrac{y – b}{x}\)

Step 3:

Solve the equation from Step 2 for y.

\(m = \dfrac{y – b}{x}\)

Multiply both sides by \(x\):

\(mx = [\dfrac{y – b}{x}]\) x \(x\)

\(mx = y – b\)

Adding \(b\) to both sides:

\(mx + b = (y – b) + b\)

\(mx + b = y\)

or

\(y = mx + b\)

Following these steps, we derive the equation of a line in slope-intercept form, \(y = mx + b\).

Example 1

Find the equation of the straight line that has slope \(m = \dfrac{-2}{5}\) and passes through the point \((4, -3)\).

Solution:

Using the slope-intercept form, which is \(y = mx + c\), we can find the equation of the line.

Given:

\(m = \dfrac{-2}{5}\)

\(x = 4\)

\(y = -3\)

Substituting the values into the equation, we have:

\(-3 = (\dfrac{-2}{5})(4) + c\)

Simplifying the right side:

\(-3 = \dfrac{-8}{5} + c\)

Rearranging the equation to find \(c\):

\(c = -3 + \dfrac{8}{5}\)

\(c = \dfrac{-15}{5} + \dfrac{8}{5}\)

\(c = \dfrac{-7}{5}\)

Now, we have the slope \((m = \dfrac{-2}{5})\) and the y-intercept \((c = \dfrac{-7}{5})\). Substituting these values into the slope-intercept form:

\(y = (\dfrac{-2}{5})x\space – \dfrac{7}{5}\)

Hence, the required equation of the straight line is:

\(y = (\dfrac{-2}{5})x\space – \dfrac{7}{5}\)

Example 2

Let’s determine the equation of a line in slope-intercept form that passes through the points \((0, 0)\) and \((2, 5)\).

Solution:

Find the slope of the line using the given points \((0, 0)\) and \((2, 5)\).

\(Slope\space m = \dfrac{(change\space in\space y-values)}{(change\space in\space x-values)}\)

\(Slope\space m = \dfrac{(5 – 0)}{(2 – 0)}\)

\(Slope\space m = \dfrac{5}{2}\)

Since the line passes through the origin \((0, 0)\), the y-intercept is \(0\).

Therefore, the equation of the line in slope-intercept form is:

\(y = (\dfrac{5}{2})x + 0\)

Simplifying the equation, we get the following:

\(y = (\dfrac{5}{2})x\)

The equation of the line that passes through the points \((0, 0)\) and \((2, 5)\) is \(y = (\dfrac{5}{2})x\).