Maths Formula Sheet
September 29, 2023

Exploring math is like uncovering the universe's secrets. At the centre of this math world is something super important called the "Maths Formula Sheet".
For students starting their math adventure, understanding the basic formulas is like having a special key. This key helps us understand algebra, arithmetic, and geometry, like the ABCs of math. But there are more complex things, like derivation, calculus, and geometry, which have special math words and rules.
We understand that remembering this mathematics formula list can feel tough. That’s why we’ve carefully compiled a big math formula sheet. It’s like your reliable friend whenever you need help with math. In this article, you’ll discover formulas from different math topics like Algebra, Calculus, Geometry, and more. We’ve also added simple math rules and explanations for handling your high school homework. So, let’s start this exciting journey and build a strong understanding of the basics of math.
Basic Math Formula List
Adding Fractions:
To add fractions, use this formula:
\(\dfrac{p}{q} + \dfrac{r}{s} = \dfrac{ps + rq}{q×s}\)
Subtracting Fractions:
For subtracting fractions, apply this formula:
\(\dfrac{p}{q} – \dfrac{r}{s} = \dfrac{ps – rq}{q×s}\)
Multiplying Fractions:
To multiply fractions, use this formula:
\(\dfrac{p}{q} × \dfrac{r}{s} = \dfrac{pr}{qs}\)
Dividing Fractions:
For dividing fractions, use this formula:
\(\dfrac{\dfrac{a}{b}} {\dfrac{c}{d}} = \dfrac{ad}{bc}\)
Proportion Rule:
When you have a proportion, \(\dfrac{p}{q} = \dfrac{c}{d}\), you can use this rule:
\(pd = qc\)
Percentage to Fraction:
To convert a percentage to a fraction, use this simple formula:
\(x\%=\dfrac{x}{100}\)
Absolute Value Formula
The absolute value of a number, denoted as \(|a|\), shows how far a number is from \(0\) on a number line. When we talk about an absolute value equation, we mean an equation that has an absolute value expression in it. Here’s the formula for absolute value:
\( |x| = x; x ≥ 0\)
\( |x| = -x; x ≤ 0\)
\(|a|\) represents the absolute value of ‘\(a\)’.
Absolute value inequalities come in two forms. One with ‘less than’, written as \(|a| < b\), and the other with ‘greater than’, written as \(|a| > b\). These two types of inequalities require different methods to solve.
Formula for the Average Rate of Change of a Function
When working with functions, we can express the Average Rate of Change of a function ‘\(f\)’ from ‘\(a\)’ to ‘\(b\)’ using function notation:
\( A(x) = \dfrac{f(b) – f(a)}{b – a} \)
Here’s what the symbols mean:
\(f(a)\) and \(f(b)\) stand for the values of the function \(f(x)\) at ‘\(a\)’ and ‘\(b\)’, respectively.
‘\(a\)’ and ‘\(b\)’ are the limits or endpoints of the function.
Cross Product Formula
The Cross Product Formula is expressed as follows:
\(a × b = |a| |b| sin θ\)
This formula calculates the cross-product or finds the angle between two vectors in various problem-solving scenarios.
Cube Root Formula
Here’s another example to illustrate:
\(8\) cubed \(= 8^3 = 512\)
The cube root of \(512 = \sqrt[3]{512} = 8\)
Hence, the cube root of \(512\) is \(8\). This signifies that \(512\) is a perfect cube.
Discriminant Formula
In the world of math, the discriminant of a polynomial is like a detective that helps us understand quadratic equations better. We call it ‘\(D\)’ or use the symbol Δ to represent it. This tells us important things about the roots (solutions) of the quadratic equation. These roots could be real numbers or tricky imaginary ones.
Imagine you have a quadratic equation like this: \(ax^2 + bx + c = 0\). Discriminant Formula is:
\(△ = b^2 – 4ac\)
X and Y Intercepts
The concept of x- and y-intercepts is not as complex as it may sound. It’s quite straightforward.
- X-Intercepts: These are the points where a graph meets and crosses the x-axis. Think of it as the place where the graph touches the ground. This point gives us information about where the graph crosses the x-axis. Mathematically, it’s where the y-coordinate is zero.
So, for the x-intercept, we have the formula:
X-Intercept = \((x, 0)\) - Y-Intercepts: Conversely, these are the points where a graph crosses the y-axis. Imagine the graph reaching up and touching the ceiling. This point tells us where the graph meets the y-axis, with the x-coordinate being zero.
Therefore, for the y-intercept, we use the formula:
Y-Intercept = \((0, y)\)
It’s important to note that you can only find one intercept in a given equation at a time. So, whether you’re looking for where the graph meets the x-axis or the y-axis, these formulas simplify the process.
Formulas of Algebraic Expressions
Algebraic expressions come in different forms depending on the number of terms and the powers of variables involved. Let’s break it down:
- Monomial: These are the simplest algebraic expressions. They consist of just one term, like \(ax, ax^2, x^3\), and so on.
- Binomial: Slightly more complex, binomials have two terms, for example, \(ax + b, ax^2 + b, ax^2 + bx\), and others.
- Trinomial: These expressions take it up another notch with three terms, such as \(ax^2 + bx + c\) or \( ax³ + bx^2 + cx.\)
Now, let’s dive into some fundamental algebraic identities that are handy to know:
- \((p + q)^2\): This identity helps us square a sum. When you expand it, you get \(p^2 + q^2 + 2pq.\)
- \((p – q)^2\): Similar to the previous one, but it’s for squaring a difference this time. The result is \(p^2 + q^2 – 2pq.\)
- \((p + q)(p – q):\) This identity is particularly useful for dividing squares. When you multiply these expressions, you end up with \(p^2 – q^2.\)
These algebraic expressions and identities are like the building blocks of algebra, and understanding them is crucial for solving more complex equations and problems.
Area Of a Circle Formula
A circle, the embodiment of symmetry and simplicity, is a geometric shape composed of points equally distant from a central fixed point known as its centre. From this centre, lines extend to the circle’s boundary, forming the radius. If you were to place two radii end-to-end within a circle, their combined length would equal that of a single diameter. Therefore, it’s worth noting that the diameter is precisely twice the length of the radius.
It’s fascinating to note that a circle occupies the maximum area among all shapes with the same perimeter. Conversely, when you compare shapes with the same area, a circle boasts the smallest possible perimeter. The perimeter of a circle, often referred to as its circumference, plays a pivotal role in understanding and working with circles.
\(Area\space of\space the\space Circle = πr^2 = \dfrac{πd^2}{4} = \dfrac{C × r}{2}\)
Binary to Decimal Formula
Converting between binary and decimal numbers might seem tricky at first, but with caution and the right formula, it’s a breeze. Just remember not to mix up these two sets of numbers!
For example, if you see the digit “\(10\)” on a page, it could represent the number “ten” if you assume it’s in the decimal system. On the other hand, those same digits “\(10\)” in binary mean “\(1\)” and “\(0\)” together, which equals the number two when translated into the decimal system.
Here’s the magic formula that helps you convert a binary number, represented as \(d_0d_1d_2…d_{n-1}\) with ‘\(n\)’ digits, into its decimal equivalent:
\((Decimal Number)10 = (d_0 × 2^0) + (d_1 × 2^1) + (d_2 × 2^2) + … + (d_{n-1} × 2^{n-1})\)
This formula is like your trusty guide for transforming binary mysteries into decimal clarity. Simply plug in the binary digits, follow the rules, and you’ll have your decimal result in no time!
Binomial Theorem Formula
When you’re faced with the task of expanding a binomial expression that’s raised to a higher power, the Binomial Theorem formula is your trusty companion. Here’s the formula:
\((x + y)^n = Σr = 0\space to\space n\space (nCr) × x^{n – r} × y^r \)
Let’s break this down a bit:
\((x + y)^n\): This is the binomial expression raised to the power ‘\(n\)’ you want to expand.
\(Σr = 0\space to\space n\): This symbol \((Σ)\) represents a summation, where you’ll add up a series of terms from \(r=0\) to \(r=n\).
\(nCr\): This part stands for “\(n\) choose \(r\)” and is calculated as \(\dfrac{n!}{(n – r)! × r!}\). It’s like a special mathematical recipe for choosing combinations.
\(x^{n – r}\): Here, you’re raising ‘\(x\)’ to the power of \((n – r)\). It’s like the changing part of your expression.
\(y^r\): Similarly, ‘\(y\)’ is raised to the power of ‘\(r\)’, providing another changing element.
In simple terms, this formula is your go-to tool to expand binomial expressions like \((x + y)^n\). It helps you break them down into a sum of terms, each with its unique combination and power of ‘\(x\)’ and ‘\(y\)’. And remember, ‘\(n!\)’ denotes the product of all the whole numbers from \(1\) to ‘\(n\)’, like \(5! = 1 × 2 × 3 × 4 × 5\).
Completing the Square Formula
In the world of elementary algebra, “completing the square” is a technique that allows us to transform a quadratic polynomial into a perfect square, accompanied by a constant term. This method isn’t just a mathematical curiosity; it’s a valuable tool for solving quadratic equations.
In fact, completing the square finds its application in various mathematical computations involving quadratic polynomials. Moreover, it plays a pivotal role in deriving the famed quadratic formula.
Completing the Square Formula is your guiding light in this process, and it takes the form:
\(Ax^2 + bx = c = (x + p)^2 + Constant\)
Exponential Formula
The exponential property is a formidable tool for untangling the mysteries of exponential equations. It empowers us to align both sides of an equation using the same base.
When we explore exponential functions, we encounter a fundamental formula:
\(f(x) = a^x\)
Here, ‘\(a\)’ represents the base, a positive number distinct from \(1\), and ‘\(x\)’ is any real number. This simple formula lays the foundation for understanding the behaviour of exponential functions.
Factoring Formulas
Factoring is the art of breaking down a number or a polynomial into a set of factors. These factors, when multiplied together, reconstruct the original value.
For the sum or difference of two nth powers, we employ specific factoring formulas to reveal their underlying structures.
\(a^n + b^n = (a-b)(b^0a^{n-1} – b^1a^{n-2} + ….. – b^{n-2}a^1 + b^{n-1}a^0)\)
\(a^n – b^n = (a-b)(b^0a^{n-1} + b^1a^{n-2} + ….. + b^{n-2}a^1 + b^{n-1}a^0)\)
Percentage Formula
The percentage formula is your go-to tool for understanding and quantifying a portion or share in terms of \(100\). At its core, “per cent” simply means “per hundred.” It’s a way to express numbers between zero and one in a more relatable manner, using a fraction of \(100\) as a reference point. This concept is denoted by the symbol ‘\(\%\)’, and it’s instrumental in comparing and assessing various ratios.
Here’s the essential formula to calculate percentages:
\(Percentage = \dfrac{Value}{Total \space Value} × 100\)
Pythagorean Theorem Formula
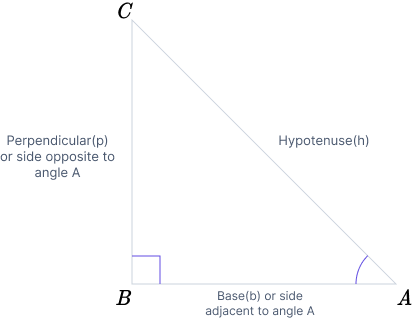
The Pythagorean Theorem stands as one of the bedrock principles in the world of mathematics. It offers profound insights into the relationships within a right-angled triangle, a concept you’re likely already familiar with. A right-angled triangle is characterized by having one angle that measures precisely 90 degrees, commonly known as a right angle. The side opposite this right angle is “hypotenuse,” while the other two sides, adjacent to the right angle, are simply referred to as the “legs.”
This theorem, often called the Pythagorean Theorem, makes a striking declaration: the square of the hypotenuse’s length is exactly equal to the sum of the squares of the lengths of those two legs. In mathematical terms, it can be expressed as:
\(Hypotenuse^2 = Perpendicular^2 + Base^2\)
Quadratic Function Formula
A quadratic function is a special kind of math equation that has a degree of \(2\). When you graph it, it forms a shape like a curve, which we call a parabola. This curve either opens upwards like a smile or downwards like a frown, depending on the equation.
Now, the most interesting part of this curve is a special point on it called the vertex. This is where the curve is either at its highest or lowest point.
In a quadratic function, the equation looks like this: \(f(x) = ax^2 + bx + c\), where ‘\(a\),’ ‘\(b\),’ and ‘\(c\)’ are just numbers, and ‘\(a\)’ can’t be zero.
To solve a quadratic function, we use this simple formula:
\( x = \dfrac{-b \pm \sqrt{b^2 – 4ac}}{2a} \)
Rate of Change Formula
In everyday language, the term “slope” refers to how steep or inclined something is. In the world of mathematics, it’s a formula we use to precisely measure how steep a straight line is. Put simply, the higher the slope, the steeper the line.
Think of slope as a way to describe the rate of change. It tells us how quickly things are changing as we move along the line. You can find the slope by connecting two points on the line and looking at how the coordinates of ‘\(y\)’ change compared to the coordinates of ‘\(x\).’
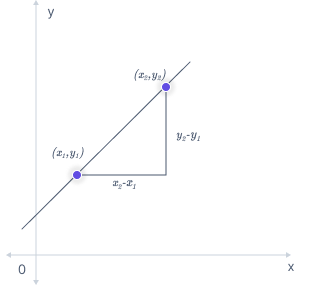
The formula for rate of change is:
\(\dfrac{△y}{△x} = \dfrac{y_2 – y_1}{x_2 – x_1}\)
Square Root Formula
The square root of a number is like a magical key that, when multiplied by itself, unlocks the original number. We represent it using a symbol that looks like a checkmark \(√\), and often, when we say “square root,” we’re referring to the principal square root, the one that’s most commonly used.
\(\sqrt[n]{x} = x^{\dfrac{1}{n}}\)
Conclusion
Math is like solving puzzles, and formulas are the special tools that help us solve these puzzles. Imagine this geometry equations sheet as a key that opens different doors to math adventures.
We know math can be tricky sometimes, and remembering all these formulas can be like remembering a bunch of passwords. That’s why we’ve made a big list of these keys, so you can use them whenever you’re stuck in a math puzzle.
So, think of these formulas as your helpful friends on your math journey. They make math less confusing and more fun!
- angles
- Area Of a Circle
- arithmetic operators
- axis
- Binary to Decimal
- Binomial Theorem
- calculus
- cross product
- Cube Root
- Discriminant
- Exponents
- factoring
- geometry
- Learn math
- Math Calculator
- math education
- Online Calculator
- percentage
- Pythagorean Theorem Formula
- quadratic
- Quadratic Function Formula
- square root
- tips and tricks
- x and y axis
- x and y intercepts
Can't find your query?
Fill out the form below with your query and we will get back to you in 24 hours.


